All published articles of this journal are available on ScienceDirect.
Agricultural Distortions and Economic Growth in Southern Africa: Evidence from Mozambique, Zambia and Zimbabwe (1970-2011)
Abstract
Introduction:
The first decade of 2000 was considered Africa’s decade of unprecedented growth as it was the fastest growing region in the world. This growth is believed to have largely been a benefit of the commodity super-cycle which is beginning to tail-off. Analysts perceive that growth in Africa is currently more threatened by global trends and region specific risks around agriculture and politics.
Statement of the problem:
It has been noted that African countries have experienced stagnant or declining agricultural productivity growth rates, increasing rural poverty, hunger and malnutrition coupled with low competitiveness in global markets over the decades.
Methodology:
Using the database on Distortions to Agricultural Incentives, the World Development Indicators and the Penn World Tables, the determinants of economic growth in Southern Africa and the impacts of a pro or anti agricultural policy regime on economic growth were investigated. In this study, three Southern Africa countries were investigated, that is, Mozambique, Zambia and Zimbabwe.
Results:
The Panel Data Analysis results suggest that 1% decrease in the degree of anti-agriculture policy bias results in a 0.1% increase in real per capita GDP. Further, 1% increase in the share of gross capital formation in GDP results in 0.04% increase in real per capita GDP.
Conclusion:
The study showed that reducing direct and indirect, implicit and explicit taxation to agriculture relative to non-agriculture sector would result in improved economic growth in the three Southern African countries of Zambia, Zimbabwe and Mozambique.
1. BACKGROUND
Agricultural policy analysis has advanced remarkably over the past five decades. One of the first innovations was the introduction of the neoclassical approach to agriculture and food policy analysis (Bullock and Salhofer) [1]. The bedrock of neoclassical agricultural policy analysis involved understanding agriculture and food policies as the use of various “instruments” to shift the price incentives of various producer and consumer groups. When analysing agriculture policies through the neoclassical lens, shifts in consumer and/or producer surplus are taken as indicators of variation in welfare outcomes between two or more groups. It is important to note that the judgement on the ranking of various policy instruments remains a normative process.
The neoclassical approach is, however, bound by certain assumptions and conditions that often do not hold in reality. These include the assumption that: the enforcement of policies is perfect and costless; there is perfect information and there are no externalities (positive or negative); and, the elasticities of factors of supply, cost shares, and substitution remain constant (Alston and James) [2]. Based on these and other assumptions, the normative neoclassical approach asserts that a market with no distortions is the best allocator of resources and would be most efficient welfare-wise.
Advances in the computational ability for data collection and analysis coupled with the rise of the theoretical branch of political economy analysis led to another landmark development in agriculture and food policy analysis. The first was the acknowledgement and the need to challenge the fallacy of the neoclassical assumptions, and hence the normative view of agricultural policy analysis. This resulted in the prominence of the Political Economy of Agriculture as a school of thought requiring further interrogation particularly in line with evaluating the welfare impacts of various policies (see Bromley [3] for a discourse).
Given the advances in economic data collection and analysis as well as the theory of political economy of agriculture, collection of a rich amount of data on agricultural and food product markets and incentives as well as the political institutions began to emerge in the 1950s (see Anderson et al. [4] for a discourse on data on distortions to incentives and Olper [5], and Aghion et al. [6] for a discourse on political institutions and agricultural incentives). The data sought to interrogate some of the unanswered political economical questions about agricultural policy in developing and developed countries. For instance, whether it is correct that the agriculture sectors of poor countries employed most of the population, yet were least supported, and if so, why the case was so (Anderson et al.) [7] and (Binswanger and Deininger) [8]. Some of the data which was collected through the World Bank’s project on Distortions to Agricultural Incentives captured the effect of direct and indirect, product specific and non-product specific support or taxation rendered by own-country and other country governments to national agriculture and non-agriculture sectors (Anderson et al.) [4].
The World Bank database was built over decades and presents advantages for more refined agricultural policy analysis. For instance, the database covers a large number of countries and commodities over a long period of time, allowing it to be used for broad cross country comparisons and hence more effectively investigates causality between various socioeconomic variables. Anderson, et al. [7] present some of the stylized facts emerging from the World Bank dataset. One of the stylized facts is that the major distortions to global agricultural trade result from rich developed countries protecting their farmers at the expense of the urban dwellers; while poor countries’ tax farmers subsidize urban dwellers (the so called, “urban bias”) (see Swinnen [9] for a richer discussion).
2. PROBLEM STATEMENT
Given that the recent rich database confirms an “urban bias” in African policy making over a relatively long period of time, this paper seeks to investigate how such a policy regime could be associated with the economic growth and development challenges experienced in Africa over the decades. According to Binswanger-Mkhize [10] African countries have experienced stagnant or declining agricultural productivity growth rates, increasing rural poverty, hunger and malnutrition coupled with low competitiveness in global markets over the decades (Binswanger-Mkhize) [10]. Nonetheless, more recently, Africa has experienced a period of sustained economic growth which has been linked by some analysts to the commodity super-cycle which could be coming to an end (World Bank) [11]. As a result, it is becoming apparent that African growth is now threatened by global trends and region-specific risks particularly around agriculture and politics (World Bank) [12]. Agriculture in particular is fragile because of its relative economic importance to the population as well as its exposure to climate change impacts (Zamfir) [13]. This paper therefore utilizes the recent datasets on agricultural distortions to investigate the relationship between agricultural distortions and economic growth.
3. LITERATURE REVIEW
3.1. Determinants of Economic Growth
There is a vast amount of literature on the determinants of economic growth, particularly in Sub Saharan Africa (SSA). However Ndulu [14], provides a comprehensive discourse on economic growth in Africa and emphasizes that Total Factor Productivity (TFP), the rate of (physical and human) capital accumulation and returns to investments strongly influence long term growth. However, the author notes that distortions and price incentives undermine the quality of capital stock and result in a negative productivity residual and weak link between physical capital accumulation and growth in most SSA countries (Ndulu) [14]. Distortions also generate inefficiencies which defer the growth objective as resources that could be used for productive purposes are channeled to rent seeking activities and corruption (Binswanger and Deininger) [8].
Ndambiri, et al. [15] concur with these findings and suggest that in addition to human capital, Research and Development (R&D) investment and Foreign Direct Investment; the economic environment and prevailing institutional frameworks have a strong bearing on growth. However, while there is consistency in theory that policies and institutions influence growth, policies are difficult to analyse because of the limitations on the availability of reliable data on policies and institutions. The developments in computational ability to collect and analyse socio economic data have allowed the building of rich datasets and composite indices that can be used in the analysis of diverse socio economic problems, such as the economic growth problem.
The building of economic datasets involving a large number of countries has enabled macroeconomists to analyse long term convergence between advanced and less advanced economies. Convergence theory asserts that there is the possibility of a tendency towards the reduction over time; of income disparities or growth rates across countries or regions. Thus, theoretical models can generate different macroeconomic predictions about long term trends in income patterns within regions depending on the underlying assumptions. It is asserted by de la Fuente [16] that convergence between poorer regions and richer regions can be explained in terms of the stability of key structural characteristics; which enable steady growth in the long run. Further to that, de la Fuente [16] highlights that being poor could be an advantage since there is no need to “reinvent the wheel” of technology and pro-poor growth policies.
Assertions however by de la Fuente [16], assume homogeneity in the stock of resources between regions which may not exist in reality. Abramovitz [17] also argues that the process of technological catch-up is far from automatic and poorer countries can instead, experience divergence of incomes and growth rather than convergence. The controversy regarding empirical growth in incomes has given ride to conditional convergence; where the underlying assumptions cannot be violated for the theory to hold (Barrow) [18].
Islam [19] highlights that the use of panel data enables the isolation of institutional and technological differences across countries or regions under consideration. Islam’s [19] panel study of a large group of countries found out the tendency of convergence for more homogenous countries and for conditional convergence but non-existent convergence for heterogeneous groups of countries. The existence of distortions in Mozambique, Zambia and Zimbabwe therefore, reduces or eliminates the tendency of convergence in both incomes and growth. In addition to distortions, de la Fuente [16] asserts that technological progress; particularly production technology can disrupt neoclassical convergence theory.
3.2. Measuring Agricultural Protection and Taxation
The database on Agricultural Distortions compiled by the World Bank, defines a distortion as the wedge between domestic prices and what they would have been in a free market scenario (Anderson, et al.) [7]. The price wedge attempts to capture the effects of direct agricultural input or output policies such as subsidies and taxes; other policies such as exchange rate over- or de-valuation and other policies in non-agricultural product sectors that might influence agricultural price incentives (Anderson, et al.) [4]. While there are many indicators within the Agricultural Distortions database, this paper uses one composite indicator, the Relative Rate of Assistance to agriculture (RRA); which is constructed from the Nominal Rate of Assistance to agriculture tradables (NRAagt) and the Nominal Rate of Assistance to non-agriculture tradables (NRAnonagt).
The Nominal Rate of Assistance (NRA) for a particular product represents the percentage by which government policies have raised/lowered gross returns to producers of that product above what they would be without government intervention (in which case the NRA would be positive/negative). In addition to support rendered on outputs, NRA includes support rendered through product-specific input subsidies and estimated level non-product specific forms of assistance or taxation. NRA for a specific group of products, for instance agricultural/non-agricultural tradables is then weighted to provide an estimate of NRAagt/NRAnonagt.
From these two indicators, the RRA can then be computed as follows:
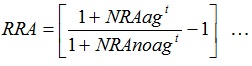 |
(0) |
Since NRAs are weighted percentages they cannot exceed -100% or 100% and hence RRA can also not exceed these bounds. However, the RRA is a particularly useful figure since it allows an internationally comparable measurement of whether a country’s sectorial policy regime has an anti- (pro-) agricultural bias (Anderson, et al.) [4].
3.3. Agricultural Distortions in Selected African Countries
Agricultural distortions have had different effects in different contexts across Africa. In Cameron, government intervention through direct and indirect fiscal taxes, the operations of marketing boards, trade and foreign exchange restrictions imposed a significant burden on farmers with urban industry benefiting in the 1970s (Bamou and Masters) [20]. Njinkeu [21] also asserts that ‘the performance of the exporting sectors in Cameroon, like agriculture, may be partly explained by the implicit tax resulting from protection of import-substituting sectors’. However, reforms in the 1980s and 1990s were a relief to farmers and the reforms included reduced subsidies to aggregators and downstream processors, with a fairly balanced taxation of processors since the 1990s (Bamou and Masters) [20]. Therefore, the reduction in agricultural taxation and removal of subsidies from processors significantly raised farmer incomes and incentives to raise agricultural production.
In Ghana, the policy landscape since the 1980s has effectively worked against farmer incentives to increase production; particularly cocoa farmers. Between 1960 and 2010, Ghana’s growth has been significantly limited by inordinate exchange rate controls, excessive state interventions and intrinsic discrimination against the agricultural sector. Recent studies by Brooks, Croppenstedt and Aggrey-Fenn [22] show that the Ghanaian government has significantly reduced agricultural distortions in form of farmer targeted taxes, but has not completely eliminated them. There is significant taxation of cocoa farmers by the COCOBOD and import-competing producers continue to receive significant protection. Brooks, Croppenstedt and Aggrey-Fenn (ibid) [22] however, note that there is no willingness on the part of government to completely eliminate distortions affecting farmers due to concerns about implications on government revenue. This therefore, reduces the ability of farmers to compete on the international market and the prospect of sustainably raising rural incomes.
In Latin America, development strategies implemented in the 1980s largely contributed to agricultural price distortions. The rationale was to catalyze economic growth through protectionist policies aimed at import-substitution industrialization (Anderson and Valdes) [23]. However, such policies in countries such as Argentina and Brazil harmed the region’s most competitive farmers through punitive agricultural export taxes. In Brazil for example, these approaches and were offset only slightly by farm credit and fertilizer subsidies as well as social safety nets for small scale farmers. It can thus, be seen in literature from Africa and elsewhere that agricultural distortions have reduced potential farmer incomes and hence, slowed down economic transformation in the rural sector.
4. METHODOLOGY
4.1. Data Sources
Secondary data was utilized for the study. The data was obtained from World Development Indicators Database (World Bank) [24], the Database on Distortions to Agricultural Incentives (World Bank) [25] (both from the World Bank) and the Penn World Tables (Feenstra, Inklaar and Trimmer) [26]. Panel data analysis was used to investigate whether distortions to agricultural incentives had a relationship with GDP growth in the three Southern African countries of Mozambique, Zambia and Zimbabwe over the years 1970 to 2011.
4.2. Model Specification
The specification of the econometric model is based on Solow’s augmented growth model as applied by Ndambiri, et al. [15] in investigating the determinants of economic growth. The explanatory variables (i.e. potential determinants of growth) include: the share physical capital formation in GDP (csh_i), human capital index (hc), share of government expenditure in GDP (csh_g), and foreign direct investment (fdi). To investigate the impact of distortions to agricultural incentives on growth, the elative rate of assistance to agriculture (rra) was introduced into the model. The RRA also describes to what extent a government’s policy position is pro- (anti-) agriculture. Therefore the model can be implicitly specified as:
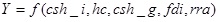 |
(1) |
Y, the dependent variable is equal to the difference in the real GDP per capita between two time periods (1970-2011). A detailed description of these variables is provided in (Table 1).
| Variable Name | Description | Source |
|---|---|---|
| Gdp | Real GDP Per Capita at Constant 2005 US$ | World Bank [27] |
| Csh_i | Share of gross capital formation at current PPPs | Feenstra, et al. [26] |
| hc | Index of human capital per person, based on years of schooling and returns to education | Feenstra, et al. [26] Barro/Lee [28] Psacharopoulos [29] |
| Csh_g | Share of government consumption at current PPPs | Feenstra, et al. [26] |
| Fdi | Foreign direct investment, net inflows (% of GDP) | World Bank [27] |
| Rra | Relative Rate of Assistance to agriculture* | Anderson, et al. [4] |
A double-log functional form was adopted for ease of interpretation as discussed by Wooldridge [30]. As such, equation (1) is explicitly presented as:
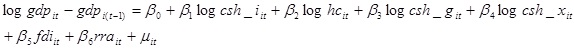 |
(2) |
Furthermore, expanding the left-hand side of the equation and rewriting it results in equation (3) shown below:
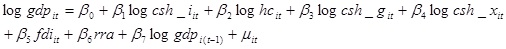 |
(3) |
It is important to note that rra and fdi are not transformed to their associated logs because of the negative values if there is net taxation of agriculture (or net outflows of FDI). This difference is taken note of in the interpretation and discussion of results. Additionally, the re-arranged equation (3) also clearly shows that levels of real GDP at time t are influenced by values of GDP in the previous time period, i.e. time t – 1.
4.3. Data Analysis
Panel data analysis methods, specifically the use of first differencing, fixed effects and random effects estimators, were applied to understand the determinants of economic growth in the three Southern African countries and to further understand whether the degree of agricultural taxation has an influence on economic growth. Running a simple pooled Ordinary Least Square (OLS) regression of equation (3) has the possible complication of failing to account for heterogeneity bias, i.e. the effect of unobserved time-varying or time-constant factors that could affect economic growth. According to Wooldridge [30], this problem can be dealt with by either estimating the parameters in equation (3) through obtaining the first differenced, fixed effects (within) or random effects estimators.
4.4. First Differenced Estimators
The first difference model allows for the existance of unobserved country-specific time-invariant (fixed) factors, represented by ai in equation (4), that may be correlated with the vector of explanatory variables discussed in equation (3), and represented as Xi in equation (4).
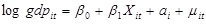 |
(4) |
From equation (4) the dependent and independent variables can be expressed in time period 1 and time period 2 and their difference as:
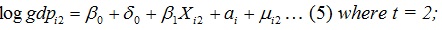 |
(5) |
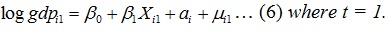 |
(6) |
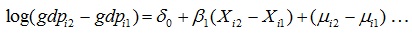 |
(7) |
In equation (5) another strength of panel data analysis is observed in that the constant is β0 in period 1 and (β0+δ0) in time period 2. Allowing the constant to vary between time periods accounts for the unobserved time varying factors that could affect the dependent variable. It can be noticed that by substrating the the t = 1 equation from the t = 2 equation eliminates the unobserved fixed effects, ai and equation (7) can be expressed as equation (8).
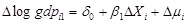 |
(8) |
By estimating equation (8) consistent estimators can be obtained as the existence of time-invarying fixed effects has been allowed and accounted for. However, regressing on the differences results in less variation in the explanatory variables which may increase the standard errors (Wooldridge) [30].
4.5. Fixed Effect/Within Estimators
Another way to account for the unobserved time-invariant factors is to use the fixed effect/within transformation. Equation (4) can also be written as:
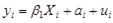 |
(9) |
Where y represents the outcome variable, log gdp. If equation (9) is averaged over time, we obtain:
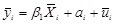 |
(10) |
The ‘bar’ shows that the variables are averaged over time, i.e. divided by the number of time periods throughout. It is important to note that the time invariant effects appear in both equation (9) and (10) because they do not change over time. Subtracting (9) from (10) therefore eliminates the unobserved effects and translates to:
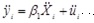 |
(11) |
Where,
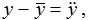 is the time demeaned variable. Estimating equation (11) then obtains the time-demeaned estimators while accounting for the time-invariant unobserved factors. These are expected to be more consistent than a simple pooled OLS.
is the time demeaned variable. Estimating equation (11) then obtains the time-demeaned estimators while accounting for the time-invariant unobserved factors. These are expected to be more consistent than a simple pooled OLS.
4.6. Random Effects Estimators
The last class of estimators that will be computed is the random effects estimators which assume the absence of any correlation between the unobserved time-invariant factors and the explanatory variables. If this is the case, eliminating the unobserved (fixed) effects would result in inefficient estimators (as opposed to the case with fixed effect or first differencing estimation). The random effect estimators have the advantage that they remain constant over time because it assumes no correlation of ai and Xi whether or not the latter varies over time (Wooldridge) [30]. In the study all estimators were computed and formal tests carried out to determine which among the three suits the structure of the data.
5. RESULTS AND DISCUSSION
5.1. Descriptive Statistics
Table 2 shows a summary of the descriptive statistics for the key variables used in the study. The average Relative Rate of Assistance to agriculture is -50.60% which shows that on average the agriculture sector in the three sample countries is taxed by approximately 50% relative to the non-agriculture sectors. This shows that an anti-agriculture bias policy orientation in these countries over the years 1970 to 2011. Foreign Direct Investment net inflows as a percentage of GDP have averaged 2.47% for the three countries over the years 1970 to 2011.
| Variable | Std. Dev. | Min | Max | Mean | Observations | |
|---|---|---|---|---|---|---|
| Real per capita GDP* | Overall variation | 0.55 | 4.96 | 6.92 | 6.21 | N = 116 |
| Between Countries | 0.64 | 5.42 | 6.63 | |||
| Year to Year | 0.22 | 5.68 | 6.80 | |||
| Relative Rate of Assistance to Agriculture | Overall Variation | 24.39 | -94.62 | 25.59 | -50.6 | N = 107 |
| Between Countries | 9.14 | -58.54 | -40.56 | |||
| Year to Year | 23.22 | -104.66 | 27.41 | |||
| FDI net Inflows as % of GDP | Overall variation | 3.56 | -0.96 | 27.62 | 2.47 | N = 116 |
| Between Countries | 1.60 | 0.74 | 3.67 | |||
| Year to Year | 3.30 | -1.78 | 26.42 | |||
| Share of Gross Capital Formation % GDP* | Overall variation | 0.55 | 0.82 | 3.48 | 2.42 | N = 126 |
| Between Countries | 0.27 | 2.12 | 2.62 | |||
| Year to Year | 0.50 | 1.13 | 3.45 | |||
| Gov. Expenditure as % of GDP* | Overall variation | 0.69 | 1.57 | 4.08 | 2.86 | N = 126 |
| Between Countries | 0.69 | 2.09 | 3.43 | |||
| Year to Year | 0.40 | 1.76 | 3.59 | |||
| Human Capital index* | Overall variation | 0.27 | 0.12 | 0.91 | 0.5 | N = 126 |
| Between Countries | 0.30 | 0.15 | 0.69 | |||
| Year to Year | 0.12 | 0.22 | 0.72 |
The table also shows the overall, within (i.e. from year to year) and between country variation for the key variables over the study period. The dependent variable, per capital GDP as varies more between the three countries than within each country from year to year. Similarly, share of government expenditure in GDP and human capital index have more variation between the three countries than from year to year. On the other hand, the Relative Rate of Assistance to agriculture, Foreign Direct Investment net inflows and the share of gross capital formation vary more from year to year within the three countries than between countries.
Table 3 shows the summary of key variables by country. Zimbabwe had the highest mean human capital development index and highest mean gross capital formation (approximately 14% of GDP) over the 42 year period. While Zimbabwe had highest average level of relative taxation on agriculture (almost 60%) and the least proportion of FDI net flows (under 1% of GDP) the country had second highest mean real per capita GDP of US$612.37 over the 42 year period. Regardless the high average per capita real GDP that the country had, Zimbabwe had the slowest economic growth rate of approximately 2.1% per annum.
Zambia had the highest mean government consumption (approximately 35% of GDP). Though Zambia had the lowest mean gross capital formation (approximately 11% of GDP) the country had the highest mean real per capita GDP of US$767.63. Among the three countries, Zambia had the second highest GDP growth rate at just over 3% per annum.
Mozambique had the highest mean level of FDI inflows (approximately 4% of GDP) relative to Zimbabwe’s less than 1% and the lowest average level of taxation on agriculture relative to non-agriculture (41%). Mozambique performed poorly in terms of human capital development and government expenditure having the lowest mean human capital index and lowest share of government consumption (only about 8% of GDP). In addition, the country had the lowest mean real per capita GDP of US$236.78 between 1970 and 2011. In spite of this, Mozambique was the fastest growing economy with a GDP growth rate of approximately 4.7% per annum.
| Human capital index | Gross capital form (% of GDP) | Gov. exp. (% of GDP) | Merchandize exports (% of GDP) | Relative rate of assistance to agric (%) | FDI net inflows (% of GDP) | Real per capita GDP (US$) | GDP growth rate (% pa) | |
|---|---|---|---|---|---|---|---|---|
| Mozambique | 1.16 | 12.76 | 8.23 | 8.51 | -0.41 | 3.67 | 236.78 | 4.67 |
| Zambia | 1.92 | 10.59 | 34.75 | 26.68 | -0.52 | 3.29 | 767.63 | 3.06 |
| Zimbabwe | 2.02 | 14.72 | 23.24 | 6.29 | -0.59 | 0.74 | 612.37 | 2.10 |
5.2. Testing for Stationarity in Panel Data
When dealing with data collected over time, such as panel data a common problem is lack of stationarity, i.e. variation of the mean and variance of the data over time. A stationary time series is one whose statistical properties such as mean, variance, and autocorrelation are all constant overtime. Most statistical forecasting methods are based on the assumption that the time series can be rendered approximately stationary (or stationarised) through the use of mathematical transformation. Before any time-related data is used for analysis it must be checked for stationarity. If it is not stationary the data has to be corrected either by first differencing the variables, de-trending the data or introducing autoregressive or moving average lags. Autoregressive lags apply when the mean of past values influence present values of a variable. Moving average lags apply when the present value of a variable is influenced by stochastic, random or unobserved factors in the past.
The dependent and independent variables were tested for stationarity using the Im-Pesaran-Shin (IPS) test for unit roots. The number of necessary lags was tested using the Akaike Information Criterion (AIC). The test for stationarity failed to reject a unit root for all variables at the 5% level of significance. The test to include any lags also tested negative and after first differencing all variables rejected to the test for a unit root at the 1% level in favour of stationarity. The results are shown in (Table 4).
| Variable | Label | IPS Z t-tilde-bar Statistic |
|---|---|---|
| d_log_gdp | First differenced log of real per capita GDP | -6.794*** |
| d_csh_i | First differenced log of share of gross capital formation | -7.155*** |
| d_csh_g | First differenced log of share of government expenditure | -7.265*** |
| d_csh_hc | First difference of log of human capital index | -7.082*** |
| d_rra | First differenced relative rate of assistance to agriculture | -5.989*** |
| d_fdi | First differenced share of FDI net inflow | -5.553*** |
Given the results presented in Table 4, equation (3) has to be re-specified as follows (where the d represents first differenced variables):
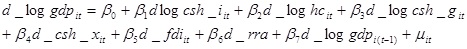 |
(12) |
5.3. Panel Data Analysis Results
Table 5 shows the results from panel data analysis. In terms of model fit, the First Difference Model estimators explain 22% of the variation in the model while the pooled OLS model explains approximately 16% of the variation in the model as indicated by the R2 values. When comparing the Fixed and Random Effects models, it is Random Effects model that explains more of the variation between countries with a between R2 of approximately 99% compared to about 76% in the Fixed Effects model. The Fixed Effect model however explains more of the variation from year to year with a within R2 of approximately 15% compared to that of 14%. The pooled OLS, Fixed Effects and Random Effects models were significant at the 5% percent level, while the First Difference model was significant at the 1% level.
| Real per capita GDP at constant prices | Pooled OLS estimators | Fixed effects (within) estimators | First difference estimators | Random effects estimators |
|---|---|---|---|---|
| a Share of gross capital formation | 0.038* | 0.036* | 0.017 | 0.037* |
| a Share of government expenditure | -0.039 | -0.040 | -0.038 | -0.038 |
| a Lagged real per capita GDP | 0.043 | 0.045 | -0.088** | 0.043 |
| Relative rate of assistance to agriculture | 0.001** | 0.001** | 0.001** | 0.001** |
| FDI net inflow as % of GDP | 0.003 | 0.003 | 0.002 | 0.003 |
| Constant | 0.003 | -0.007 | 0.002 | |
| R2 | 0.155 | 0.216 | ||
| Prob > F | 0.026 | 0.039 | 0.002 | 0.018 |
| R2 – within | 0.163 | 0.151 | ||
| R2 – between | 0.757 | 0.999 | ||
| R2 – overall | 0.134 | 0.155 | ||
| Sigma u | 0.018 | 0.000 | ||
| Sigma e | 0.058 | 0.058 | ||
| Rho | 0.088 | 0.000 | ||
| Theta |
***significant at 1% level
**significant at 5% level
*significant at 10% level.
With regards to testing the hypothesis of the determinants of economic growth, the analysis shows that reducing the degree of taxation on agriculture relative to non-agriculture sector in the three Southern African countries is significantly associated with positive economic growth. Given that the RRA is expressed in percentage terms; the coefficient on the RRA of 0.001 implies that a single percentage increase in the relative rate of assistance to agriculture results in a 0.1% increase in real per capita GDP. Given that the results are significant at the 5% level across the different models, these results apply for country to country comparisons as they do for year to year variation. Therefore, if one country increases its RRA by 1% relative to other countries, its GDP would grow by 0.1% relative to other countries. Similarly, if a country would increase its RRA by 1% from one year to the next, its GDP would grow by 0.1%.
The share of gross capital formation in GDP is also significantly associated with increased economic growth. A unit increase in the share of gross capital formation in GDP results in an increase in real GDP per capita of approximately 0.04% (almost half of the change that would be expected from reducing relative taxation of agriculture by 1%). However, for the three countries, other variables do not significantly influence real per capita GDP, except the lagged value of GDP if the First Difference estimators are used. Rho is the proportion of variation explained by the individual specific effects. The results showed that approximately 9% (if the fixed effects model is used) of the variation is due to individual specific effects. This implies that approximately 90% of the variation in the data is due to the idiosyncratic randomness and not the individual specific effects.
6. DIAGNOSTIC TESTS
The Haussman test for fixed versus random effects showed that there was no significant difference between random effect and fixed effect estimators hence the random effect estimators are preferred. The Breusch-Pagan LM test for random effects also showed that there is no significant difference between the pooled OLS estimators and the random effects estimators. Given these results, the interpretation on the effect of RRA on growth is not affected given that all four models were observed across all estimators.
CONCLUSION
The study showed that reducing direct and indirect, implicit and explicit taxation to agriculture relative to non-agriculture sector would result in improved economic growth in the three Southern African countries of Zambia, Zimbabwe and Mozambique. This supports the findings of Anderson, et al. [7] and Anderson, et al. [4] who assert that reducing distortions to agricultural incentives results in higher welfare outcomes. The results; however, do not prove that increased protection is accompanied by increased economic growth. Additionally, the results do not show the specific forms of taxation that must be reduced. However, from literature some of the growth hampering forms of agricultural taxation include trade barriers such as import/export tariffs imposed by country governments and non-trade barriers such as special safety guards, safety restrictions and preferential market access arrangements imposed by other countries.
RECOMMENDATIONS
The fact that distortions arising from other countries also affect growth in the local context calls for regional and international cooperation in reducing distortions to agricultural incentives. The results concur with Ndulu’s study [14], who emphasizes that sustained growth in African economies requires investment incentives for capital accumulation and reduction of distortions, particularly reducing transaction costs and relieving capacity limitations.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No Animals/Humans were used for studies that are base of this research.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors (Douglas Ncube, PhD) certify that they have no affiliations with or involvement in any organisation or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership; employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.
ACKNOWLEDGEMENTS
The author thanks Harrison Manyumwa for the technical assistance provided when writing up this manuscript.


